Orbital motion in PICO-8

Modelling gravity is a lot of fun and a great excuse for a hours PICO-8 programming.  In this post I will take you through a very simple orbit model that uses Newton’s inverse square law of gravitation to model planetary motion.

The key to gravitation is held in Newton’s law which states that the force between two objects of mass m₁ and m₂ is inversely proportional to the square of the distance (r) between them.  The constant of prportionality is G and is a tiny number (6.674×10⁻¹¹ m³ kg⁻¹ s⁻² which explains why there is no measurable gravitational force between people):

To model this is PICO-8 we need to calculate the distance between two objects.  PICO-8 has no built in function to do this, but if you know the coordinates of the two objects, you can use pythagoras to calculate the distance (the hypotenuse) between the two.

I add a pythag(a,b) function to my projects to keep things simple.

function pythag(a,b)
  return sqrt(a^2+b^2)
end

I then use this to calculate the distance between the two objects (here called sun and p (for planet))

dist=pythag(sun.x-p.x,sun.y-p.y)

Because pythag() involves squaring the difference in x and y values, it doesn’t matter which way around the sun and p object are.

Now we have the distance, we can calculate the force acting on the planet.  Note that we make a few assumptions here to keep things easy.  First, we assume the planet’s mass is unimportant in comparison to the sun.  Secondly we combine G and m₁ into a single value of 20.

force=((1/(dist^2))*sun.g)/10

Finally, to get everything working within PICO-8’s 128 pixel square I divide the field strength by 10.

Now we have the force we need to break it down into the x and y components.  Every update cycle, we move the planet a certain distance in the x and y directions using to velocity vectors vx and vy.

To calculate the components for these two vectors, we need the direction of the force and for this we use atan2 which calculates the inverse tangent of the ratio of dx/dy.  A full explanation is here.

angle = atan2(p.x-sun.x,p.y-sun.y)

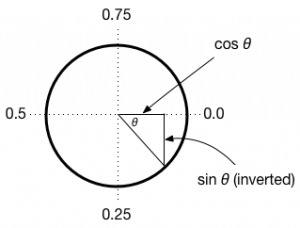
As you can see above, PICO-8 represents this angle as a value from 0 to 1, but this doesn’t matter too much as we will simply be taking the cos and sin of this value to give us the components in the x and y direction:

p.vx=p.vx-force*cos(angle)
p.vy=p.vy-force*sin(angle)

Finally, we move the planet by updating the x and y coordinates by the vectors vx and vy:

--move
p.x+=p.vx
p.y+=p.vy

I’ve attached a cart here that adds a little more (including more planets).  Download it here: solar v2.