Collisions between objects using line intersection

Collisions are always one of the more difficult aspects of computer game programming.  One very useful method of determining whether one object has hit another is to check whether two lines cross each other.

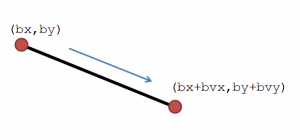
As an example, consider a bullet (b) located at coordinates bx and by which travels at a velocity in the x and y axis of bvx and bvy.  This is shown in the diagram below and you can see that the movement of the bullet follows a line finishing at the position {bx+bvx, by+bvy).

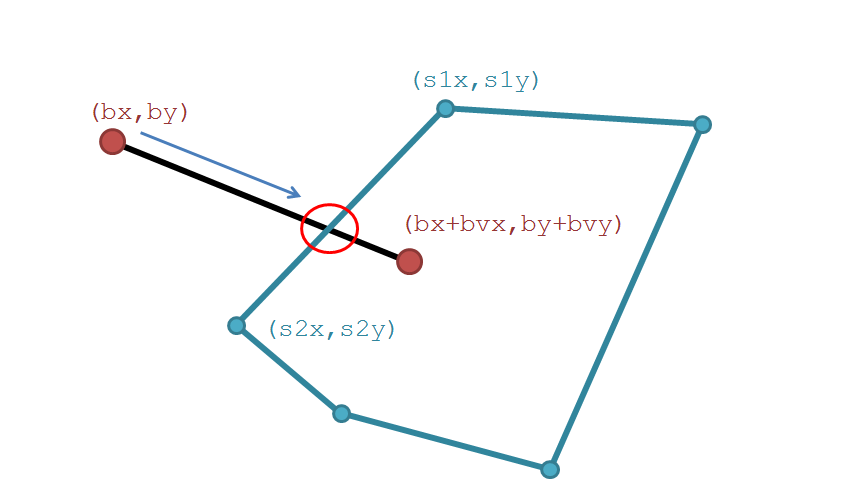
If we have another object with edges as shown in the figure below, we can check for whether the line described by the bullet crosses with the line described by the edge of the object (shown as a red circle).  The bonus of this method of calculating collisions is that you can obtain the exact coordinates of any collision and use this for further, more exciting, options in your game.

Languages such as GameMaker provide plenty of collision based functions such as collision_line or point_in_rectangle. Even these may not give the exact coordinates of a collision, instead returning a boolean answer.

In order to find where two lines cross we need to calculate the straight line formula (y=mx+c) for the two lines.  For this I write a function that requires the start and end coordinates of the line (In this post I use PICO-8 to describe the function, but the mathematics and structure are applicable to GameMaker or any other language):

function get_line_data(x1,y1,x2,y2)
  local l={}
  l.m=(y2-y1)/(x2-x1)
  l.c=-(l.m*x1)+y1
  return l
end

This returns a linear equation data type with two variables: m for the gradient and c for the y axis intercept.  The gradient is simply calculated as dy/dx.  The value for c is calulcated by feeding this value of m back into one of the sets of coordinates (a full explanation can be found here).

This linear equation data type is important as we use it in the next function which gives the coordinates of the location where the two lines meet.

function lines_cross(l1,l2)
  local i={}
  local tm = l1.m-l2.m
  local tc = l2.c-l1.c

  --are they parallel?
  if l1.m==l2.m then 
   i.cross=false 
   i.x=0
   i.y=0
  else
   i.cross=true
   --x intercept 
   i.x = tc/tm 
   --y intercept 
   i.y = l1.m*i.x+l1.c 
  end
  return i
end

This function takes two linear equations (that is a pair of variables relating to m and c) and outputs a coordinate for the meeting of the lines.  If the two lines cross, they will share a set of x,y coordinates and so this function churns the maths required to calculate this.  Two parallel lines never meet (or meet at infinity, which is probably out of the scope of your game), so the function returns a third value as well as the coordinates (cross) which is set to true if the lines cross.

We are nearly there now, but all we have established so far are the coordinates (or otherwise) of interception of two lines.  The final piece of the jigsaw is to determine whether the lines cross in the range of the two lines.  The figure below shows the difference:

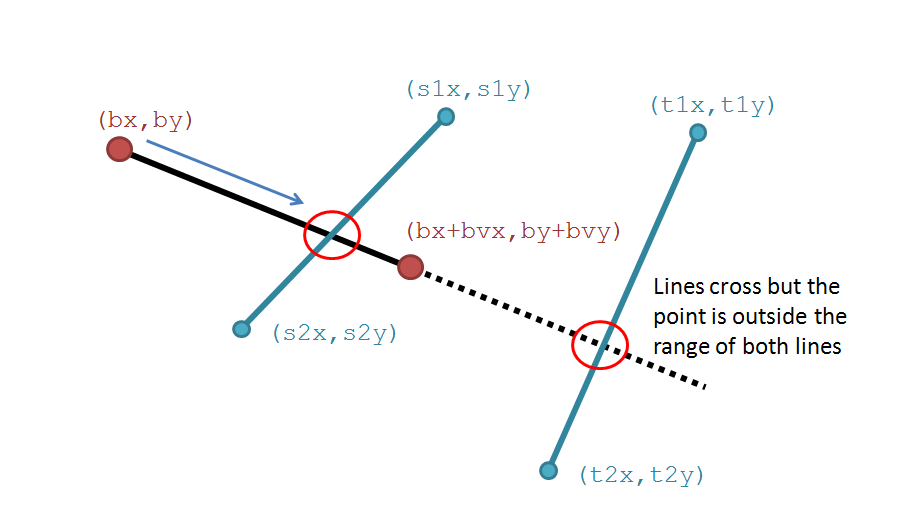
So, we finally check if the coordinates are within the bounds and for this we send the coordinates (x and y) and two sets of line data (x1,y1 & x2,y2).  To keep it neat, I wrap all three of these into tables (PICO-8) or whatever data type system you may like.

function in_range_lines(coord,lin1,lin2)
  local bmax_x=max(lin2.x1,lin2.x2)
  local bmin_x=min(lin2.x1,lin2.x2)
  local bmax_y=max(lin2.y1,lin2.y2)
  local bmin_y=min(lin2.y1,lin2.y2)
  local smax_x=max(lin1.x1,lin1.x2)
  local smin_x=min(lin1.x1,lin1.x2)
  local smax_y=max(lin1.y1,lin1.y2)
  local smin_y=min(lin1.y1,lin1.y2)
  local cross=true
  
  if (coord.x>bmax_x or 
        coord.x<bmin_x or
        coord.y>bmax_y or 
        coord.y<bmin_y) or
        (coord.x>smax_x or 
        coord.x<smin_x or
        coord.y>smax_y or 
        coord.y<smin_y) then
    cross=false
  end
  
  return cross
end

Basically, we check if the coordinates fall into both lines.  If they do we have coordinates and we know they represent where two lines cross.

In order to merge it into a project I have written a single PICO-8 function that returns a table containing three variables:

c: boolean - do the lines intersect
x: the x coordinate of the intesection
y: the y coordinate of the intesection

The code is below.  Please use it and enjoy!

function line_intersect(ax1,ay1,ax2,ay2,bx1,by1,bx2,by2)
  --output
  out={}
  out.cross=false
  out.x=0
  out.y=0
  
  --linear equation
  local l1={}
  local l2={}
  
  l1.m=(ay2-ay1)/(ax2-ax1)
  l1.c=-(l1.m*ax1)+ay1
  l2.m=(by2-by1)/(bx2-bx1)
  l2.c=-(l2.m*bx1)+by1
  
  if l1.m==l2.m then
    --parallel
    return out
  else
    --coordinates of cross
    local tm = l1.m-l2.m
    local tc = l2.c-l1.c
    
    --x intercept
    local ix = tc/tm
    out.x=ix
    
    --y intercept
    local iy = l1.m*ix+l1.c
    
    
    --finally, check the range
    local amax_x=max(ax1,ax2)
    local amin_x=min(ax1,ax2)
    local amax_y=max(ay1,ay2)
    local amin_y=min(ay1,ay2)
    local bmax_x=max(bx1,bx2)
    local bmin_x=min(bx1,bx2)
    local bmax_y=max(by1,by2)
    local bmin_y=min(by1,by2)
    
    if (ix>amax_x or 
      ix<amin_x or
      iy>amax_y or 
      iy<amin_y) or
      (ix>bmax_x or 
      ix<bmin_x or
      iy>bmax_y or 
      iy<bmin_y) then
    out.cross=false
  else
  	out.x=ix
  	out.y=iy
  	out.cross=true 
  end
  end	
  return out	
end

 

Happy programming!